We all have seen graph papers having never ending array of tiny squares with great amazement and wonder. In mathematical terms, we would call it a “periodic tiling of space”, which has shapes covering an entire area with no overlap and neither a gap. Now move the paper by the length of a tile or rotated it by 90 degrees, you will have the same pattern. The reason being that the whole sheet has the same symmetry as a single tile on it. Now take a pentagon instead of a square – and you will soon find out that it’s impossible to make a similar pattern simply because the pentagons won’t fit together without overlapping one another or leaving quite apparent gaps in between.
Patterns like these and crystals which are made up of atoms or molecules are similar in their symmetries. You will be amazed to know that these sort of arrangements are preferred in nature because as they require the least amount of energy to assemble.
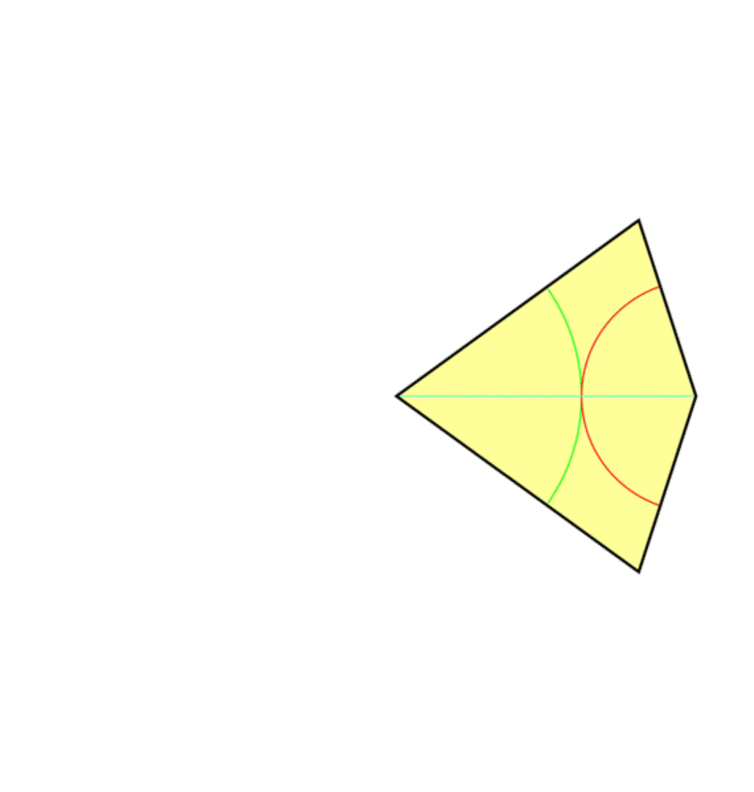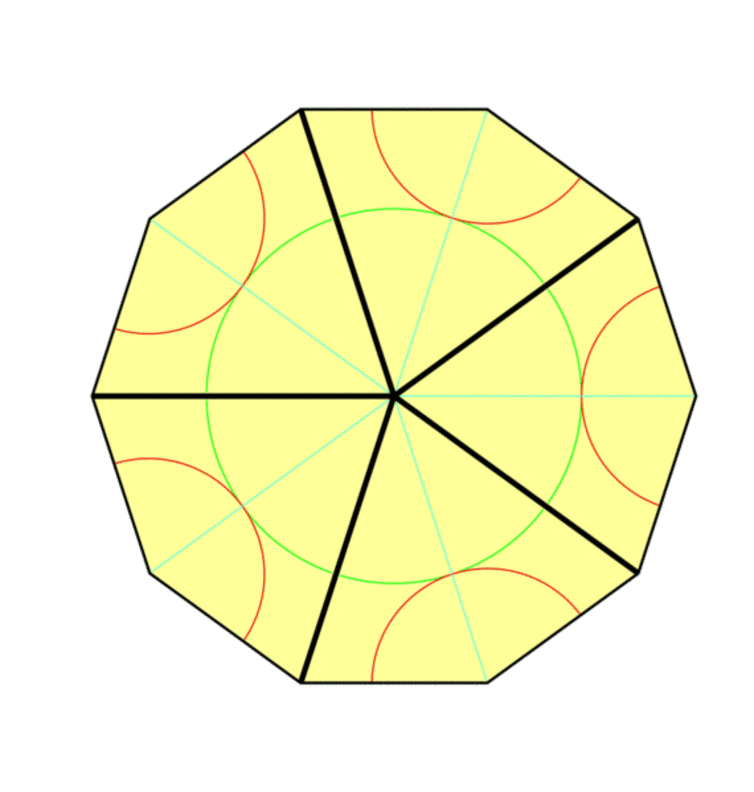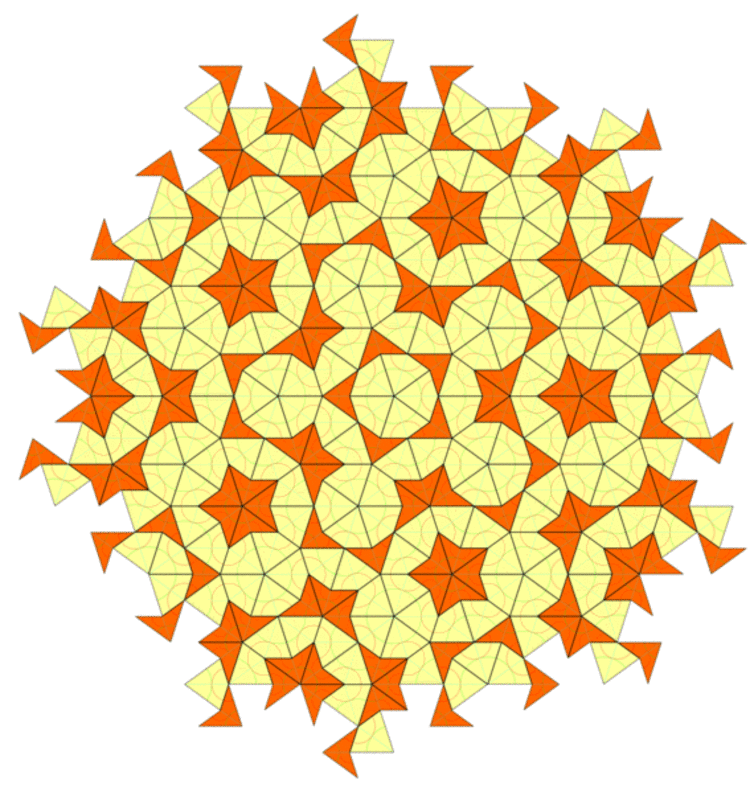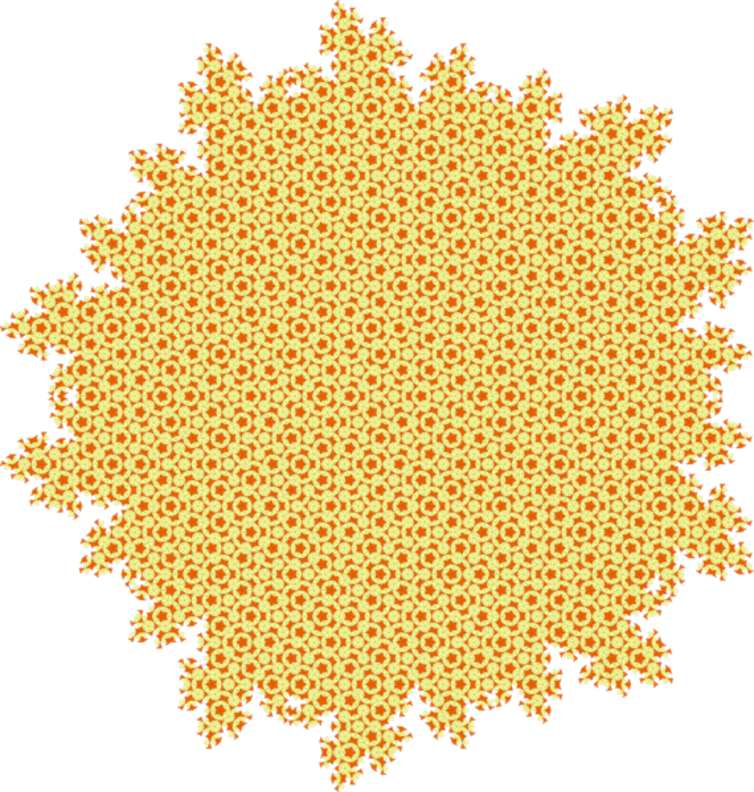
Today we will base our logic on the findings of a physicist named Roger Penrose. In 1970 he discovered that the possibility of making a pattern from two different shapes which have the angles and sides of a pentagon. And this is the trick behind making different patterns from the same shape. It looks the same when rotated through 72-degree angles, which means that it will still look the same if you rotate it 360 degrees from five different angles. For example, in the gif below, the five-pointed star is used over and over again. But since these stars are surrounded by different shapes every time, the whole pattern never repeats in any direction. This is a classic example of a pattern that has rotational symmetry but no transnational symmetry.
Irrational number
Now coming to the mathematics of the phenomenon. The property of having never-repeating pattern of a crystal with rotational symmetry but no transnational symmetry arises from an irrational number. To elaborate, take a regular pentagon. The pentagon should be such that it has the golden ratio. Which means the ratio of the side length of the five-pointed star you can draw inside a pentagon, to the side of the actual pentagon should be equal to the famous irrational number “phi” or 1.618 (not pi). The golden ratio also satisfies the relation phi = 1+1/phi. Consequently, as you can see in the picture below, when a quasicrystal is constructed with tiles that are derived from a pentagon we observe rotational symmetry at 72-degree angles.

This five-fold symmetry can be found in the image of the quasicrystal as the ten radial lines around the central red dot (above). The white balls can be though of as the location of atoms in the crystal structure while the red and yellow rods are there to represent bonds between particles, and the shapes and symmetries of the structure.
The above two features are needed to form a 3D quasicrystal. The first is the requirement that the patterns at two different sizes occuring at an appropriate irrational ratio (e.g. phi) should both occur in the system. And the second requirement is that these patterns should be able to influence each other’s appearance. Other regular crystal structures like hexagons, body-centered cubes etc. can also be formed besides the never repeating structures. These models allow us to explore the possibilities of all these different patterns and also to pin point the conditions under which quasicrystals will be formed in nature.
The mathematics is not just in theory, but is also very important for many practical applications, including making very efficient quasicrystal lasers and home paint finishing. That is why the researchers at the University of Leeds were intrigued enough to dive into this phenomenon and bring out this wonderful answer for us.
Have anything else to add to this article? Let us know in the comments’ section below!


