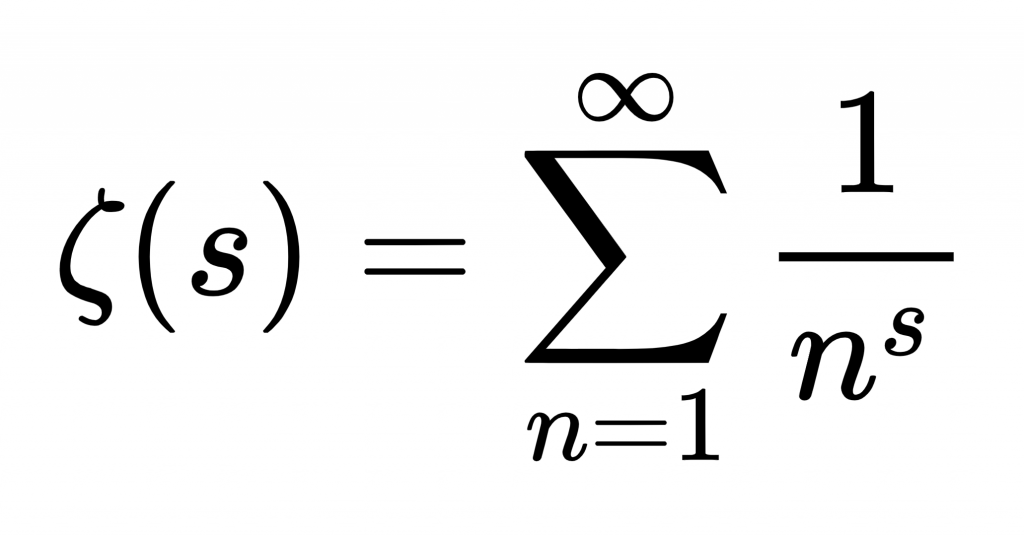Zhang Yitang is from Shanghai and is a professor of mathematics at the University of California, Santa Barbara. He has submitted a 111-page manuscript for a peer review. If it comes through, he might become the first person to solve the Riemann hypothesis, The South China Morning Post (SCMP) has reported.
The Riemann hypothesis is a 150-year-old puzzle that was published in 1859.
Riemann hypothesized that prime numbers do not occur erratically but rather follow the frequency of an elaborate function, which is called the Riemann zeta function. Using this function, one can reliably predict where prime numbers occur, but it has not been proven as of now.
Zhang worked in the fields and factories for many years to make his way to Peking University, where he got his master’s degree in 1984.
He moved to the U.S. to get a Ph.D. in mathematics from Purdue University. Zhang then worked as an accountant, a restaurant manager, and even a food delivery person before getting a position to teach pre-algebra and calculus at the University of New Hampshire in 1999, the SCMP report said.
In 2013, Zhang became famous for presenting his twin prime conjecture, which proposed that there were an infinite pair of prime numbers that differed by two.
If his paper gets approved and published now, it would end another famous mathematical hypothesis, the Landau-Siegel conjecture.
This conjecture was brought forward by Edmund Landau and Carl Siegel. It talks about the existence of zero points of type of L-functions in number theory. To make it simple, the conjecture provides counterexamples to the Riemann hypothesis.
Zhang is expected to present his work at a lecture at Peking University today, and the publication could possibly enter the peer review process this month, the SCMP report said. If the process goes smoothly, Zhang will receive a $1 million prize from the Clay Mathematics Institute.
It is important to note that similar claims have been made earlier by professors too. They included a mathematics professor in India and Sir Michael Atiyah but both papers did not succeed.