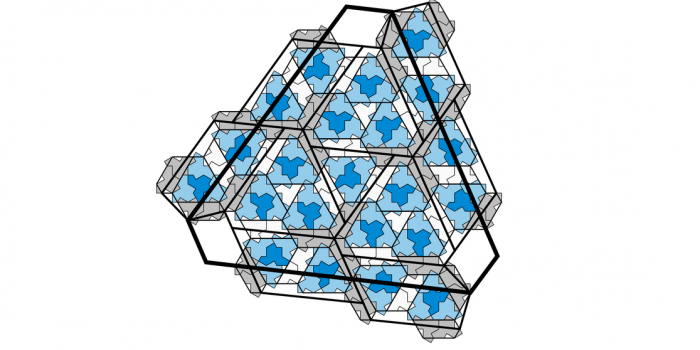
A group of computer scientists has made a significant breakthrough in the world of aperiodic monotiles, finding a shape called the “einstein” that can cover a plane without ever repeating a pattern.
This unique shape has only 13 sides and is known as an “aperiodic monotile” because it can tile a plane without ever repeating. Craig Kaplan, a computer science professor from the University of Waterloo, and his team called the shape “the hat,” a polykite that must assemble into tilings based on a substitution system. They used computer coding to prove the nature of the shape, and interestingly, the shape doesn’t lose its aperiodic nature even when the length of the sides changes.
Chaim Goodman-Strauss, a University of Arkansas professor and team member, likened finding the einstein shape to “looking for a one-in-a-million thing,” noting that the team had to filter out the vast majority of boring shapes to find something worth exploring.

The team’s discovery of the einstein shape is a major achievement in the world of aperiodic tiles, surpassing previous discoveries that had over 20,000 tiles. Kaplan notes that subsequent research has lowered that number, with sets of size 92, then six, and then two in the form of the famous Penrose tiles from 1974. However, nobody had found an einstein shape until Kaplan and his team did so.
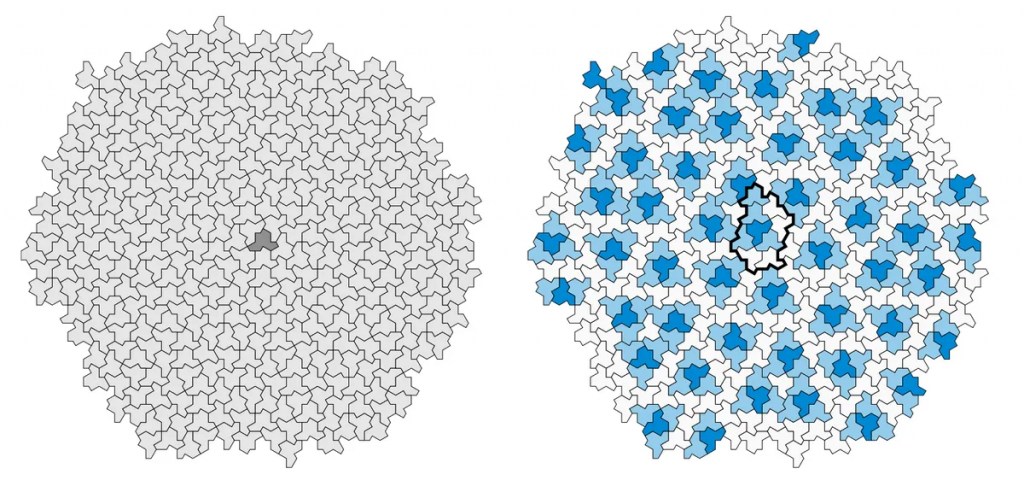
The discovery of the einstein shape is a significant breakthrough in the field of aperiodic monotiles, demonstrating that a single shape can tile a plane aperiodically. This finding has potential implications for the development of tiling patterns in the future.
As Kaplan puts it, “We finally got down to one!”