We all have learned about the number line during our time in school. There doesn’t seem to be much going around on it; just a line with markings for numbers. However, in reality, it is a very happening place that is filled with interesting problems. Among these problems is the problem known as the sum of three cubes problem.

The problem states that whether any whole number on the number line, negative or positive, can be expressed as the sum of three cubes. For instance, k= x3 + y3 + z3 where k is a whole number. So, 29 and 26 can be written like this;
29 = 33 + 13 + 13
26 = 114,844,3653 + 110,902,3013 + –142,254,8403

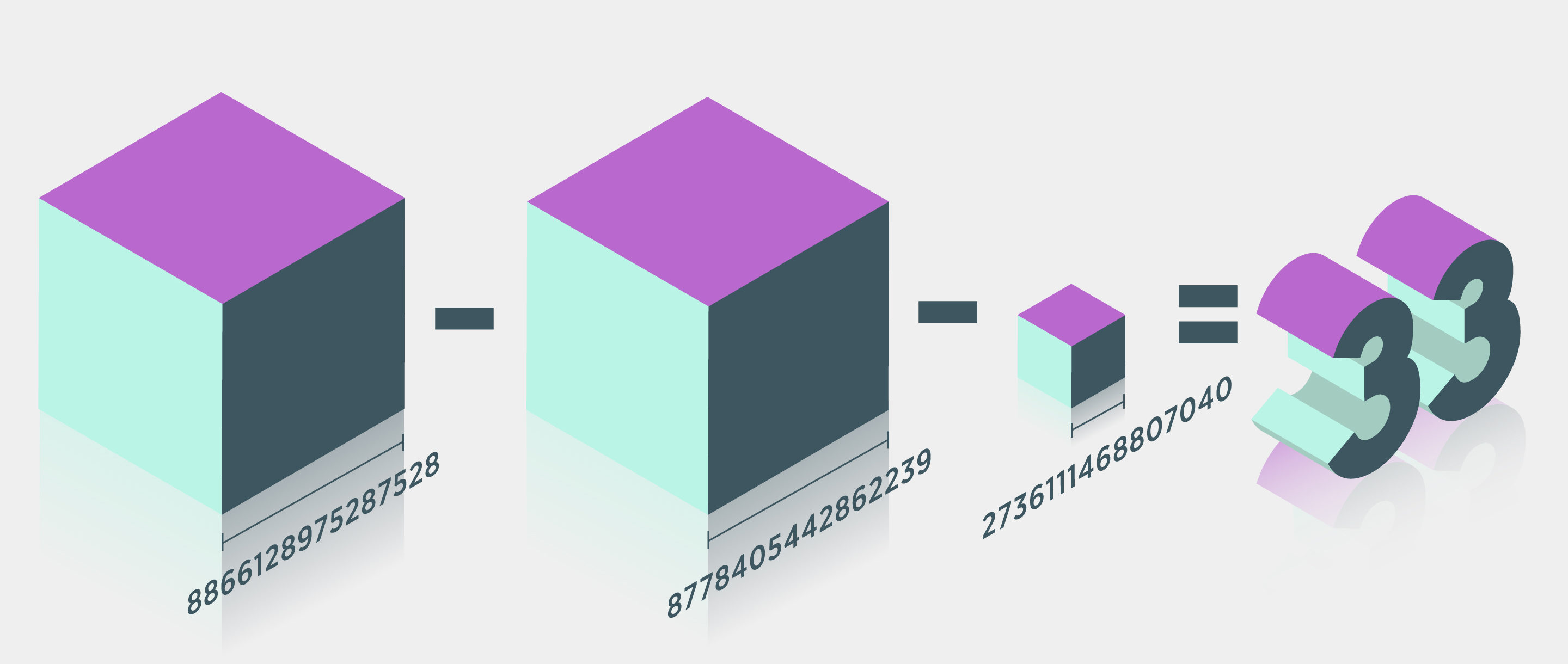
However, there are numbers that cannot be written in this sum of three cubes form. Such numbers include the whole numbers that give a remainder of 4 or 5 when divided by 9. The answer to many whole numbers that can be expressed in the sum of three cubes form have been known; the number 33 has remained a mystery for over 64 years. However, Andrew Booker, a mathematician at the University of Bristol, has taken a crack at the problem and found a solution. He discovered that 33 can be written as 8,866,128,975,287,5283 + –8,778,405,442,862,2393 + –2,736,111,468,807,0403.

Booker has solved the problem by coming up with a brand new search algorithm. He had this algorithm run on the university’s supercomputer for a total of three weeks. He does say that originally he had thought that the solution would take about six months to solve. As per Booker, his algorithm is a much more efficient approach to locating solutions for the sum of three cubes problem. In fact, he claims that it might be twenty times faster as opposed to earlier algorithms.
Up until Booker had found the solution of number 33, only two numbers below 100 had remained unsolved; 33 and 42. Number 42 has become famous ever since Douglas Adams’ The Hitchhiker’s Guide to the Galaxy came out stating that ‘the answer to the ultimate question of life, the universe and everything is 42.’