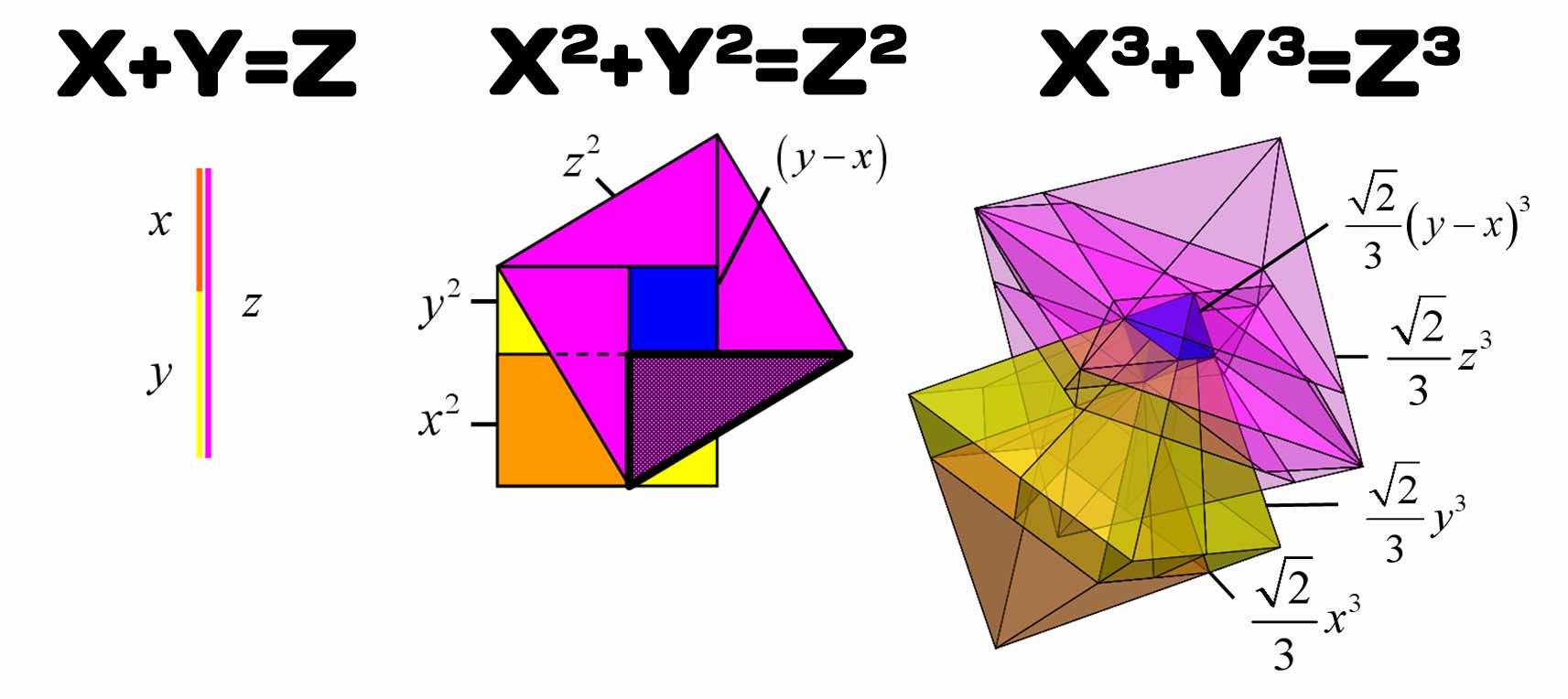The one theorem that almost anyone who has ever studied Mathematics remembers is the Pythagoras’ theorem. It is the most well-known theorem for about 2,500 years now and has allowed the mankind to evolve in a myriad of ways. Its applications are limitless and range from construction to even evaluating the atomic structure of a crystal. However, up until now, it was bound to 2D only.

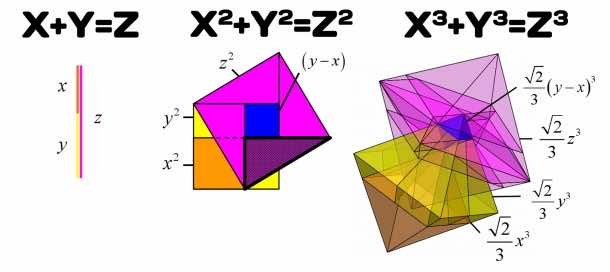
For the last 5 years, an aerospace and aeronautics engineer Luis Teia has been on a quest to understand the Pythagoras’ theorem in 3D. Using his paper, “Pythagoras triples explained via central squares” that was published in the 2015 edition of Australian Senior Mathematics Journal, he has derived the proof.
Okay, sounds amazing but what on Earth does it really mean? Before we jump into the details, the 2D proof of the theorem required about half a page, right? For the 3D proof, a book of 120 pages is required – that’s how complex it is. The geometrical part was drawn by making use of CAD and the algebra covers the 2/3rd of the book. Both, 2D and 3D, proofs are interconnected and the 3D proof is, in fact, built using the 2D one in a particular way.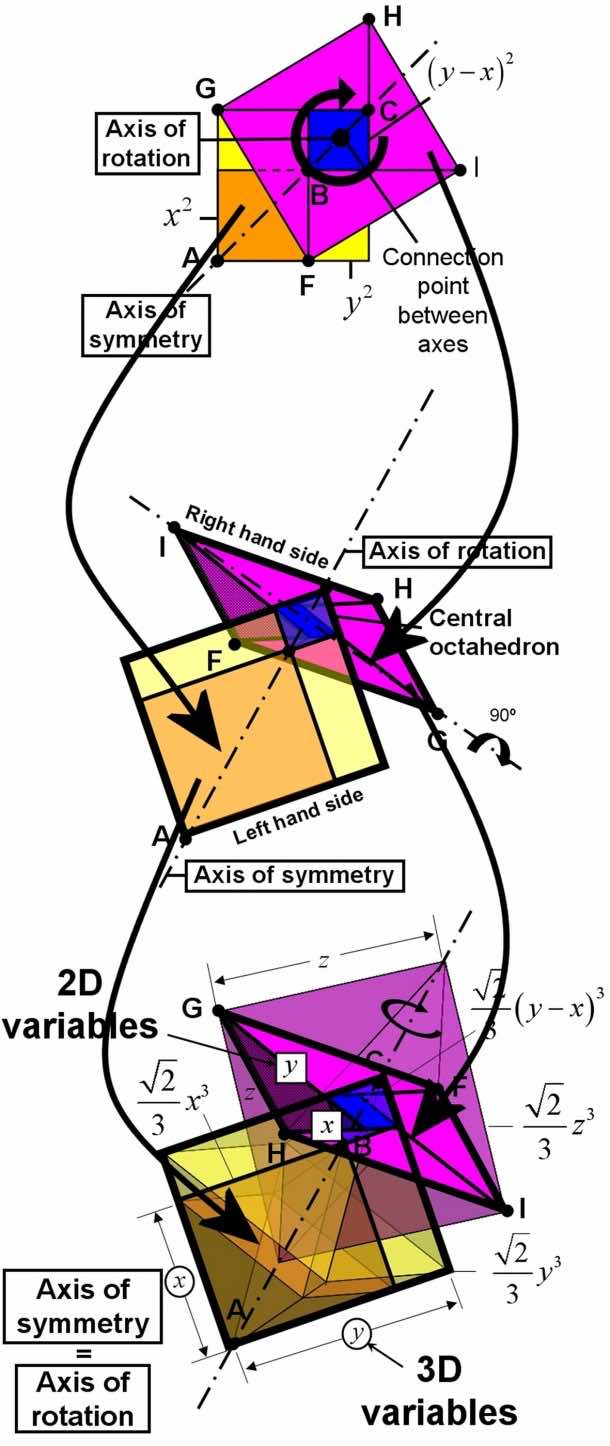
The right-hand side of the theorem is rotated by 90 degrees and the blue square transforms into a blue octahedron. For those who do not know, an octahedron is the 3D equivalent of a square. This implies that while the 2D proof is based on squares, the 3D proof relies on octahedrons. One can spot the presence of 2D theorem by understanding that right-angle triangle (shaded) is present. The 3D variables are in fact governed by the 2D. The detailed explanations can be found in Teia’s book, X3+Y3=Z3: The Proof.
The benefits of this? This recent understanding can help us in reaching an enhanced 3D version of our current geometry and would help mankind embark on our technological leap similar to the one that Pythagoras helped achieved about 2.5 millennia ago.