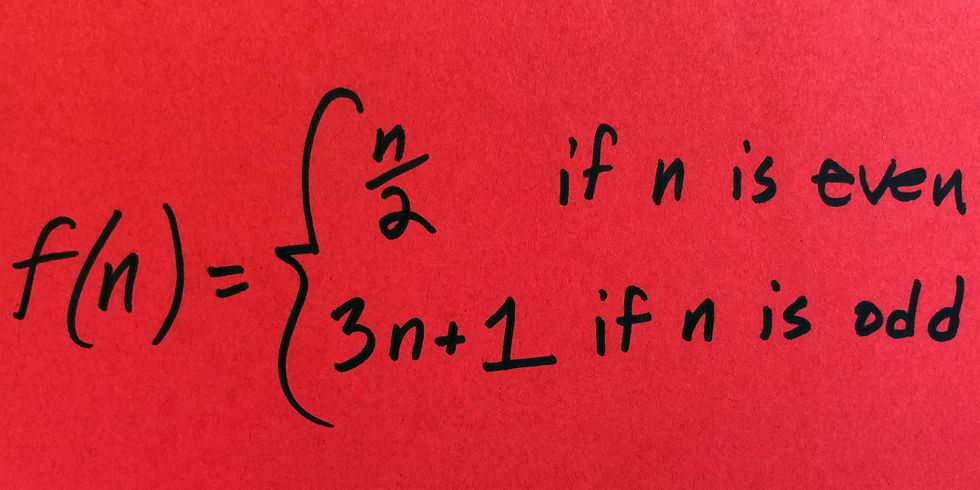We recently celebrated the answer to a decades-old mathematics problem. And here we are again to celebrate another small victory that has brought us closer to solving Collatz Conjecture. Collatz Conjecture is a numbers problem that is even older and has been giving even the brightest minds the run for their money. Despite this small step towards the solution to the problem, almost all mathematicians agree that the complete answer to this 82-year-old math riddle is quite far away.

Terence Tao is among the greatest mathematicians of our time. He got his Ph.D. at the age of 21 at Princeton. At 24, he was the youngest math professor at UCLA ever. Back in 2006, he won the Fields Medal – Nobel Prize of math – at the young age of 31. What really sets Terence apart is that he really delivers on content. What’s more, is that he shares it openly with everyone. His blog can be described as a modern-day da Vinci’s notebook.

The problem that we are going to be discussing is Collatz Conjecture. It was proposed back in 1937 by German mathematician Lothar Collatz. Collatz Conjecture can be described rather easily. Pick any natural number and then apply a function to it. This gives you the next number and so on and so forth. The rule for this is this; if the number is even, you divide it by 2. If the number is odd, then you multiply by three and add 1.
This is what it looks like in a closed format;

For instance, say you chose 10. Since it is even, you will divide it by two thus leaving you with 5. Now it is odd, so you will multiply it by three and then add 1. The resulting number is 16. Now you will again divide it by two thus giving you 8. Halving it again will give you four so will divide it again and this goes on until you end up at 1. The Collatz Conjecture says that regardless of the number you start with, you will inevitably end up at 1.
Tao’s breakthrough post has been titled, ‘’Almost All Collatz Orbits Attain Almost Bounded Values.’ What Tao is trying to say in this blog post is that counterexamples to the Collatz Conjecture are very rare. In the comment section of the blog post, he said, ‘one usually cannot rigorously convert positive average case results to positive worst-case results, and when the worst-case result is eventually proved, it is often by a quite different set of techniques.’ This means that while this method might bring us closer to the solution, the complete solution might require a completely different approach.